Struktur Data : Infix to Postfix Expression

  Dalam materi sebelumnya telah kita bahas konsep dasar dari infix, postfix dan prefix. kali ini kita akan membahas tentang algoritma untuk mengonversi dari infix ke postfix. Dari materi sebelumnya telah kita ketahui caranya namun saat ini kita akan coba dengan manual.

  Untuk mengonvert dari infix ke postfix kita akan dahulukan operator kemudian akan disusul oleh operand.
Langkah operasi :
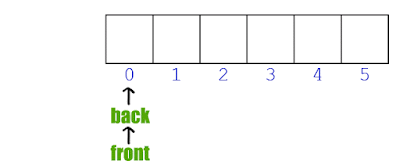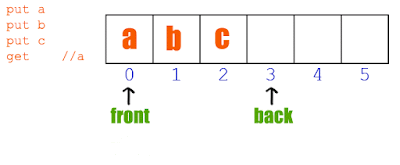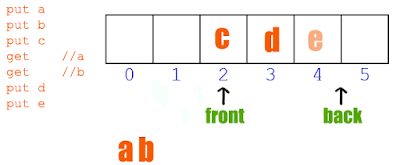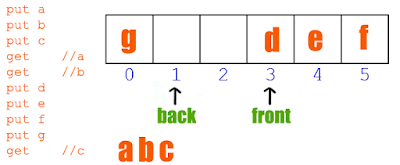
1. Buat sebuah stack untuk menyimpan operator. buat list kosong untuk menampung hasil.
2. Pisahkan inputan infix dalam bentuk string dengan menggunakan metode split.
3. Kita periksa token list dari kiri ke kanan.

• jika token adalah operand, append kedalam output list.
• jika token adalah kurung buka "(", push kedalam stack.
• jika token adalah kurung buka ")", pop (keluarkan) isi stack sampai kurung buka dikeluarkan. append setiap operator kedalam output list.
• jika token adalah operator, *, /, +, atau -, push kedalam stack. namun, pertama-tama hapus semua operator yang sudah ada di stack yang memiliki prioritas yang lebih tinggi atau sama dan append ke dalam output list.

4. Setelah inputan telah kita proses, cek stack. lalu keluarkan semua isinya dan masukkan kedalam output list.

  Algoritma pemrograman yang diimplementasikan ke dalam bahasa Pyhton beserta penjelasannya (disetiap baris code) bisa di perhatikan gambar di bawah ini : 
full source code :

penjelasan dalam code:

Langkah 1 & 2

Langkah 3 & 4

  Sekian materi untuk korversi dari infix to posfix yang bisa kami sampaikan, mohon maaf apabila terdapat kekeliruan dalam pengetikan algoritmanya, kami menerima saran dari kalian langsung saja komentar di kolom komentar di bagian bawah postingan ini 😁. Sampai jumpa di materi selanjutnya 😍.

Read More

Struktur Data : Postfix, Infix, Prefix

Hai semua kali ini kita akan membahas sesuatu hal penting dan merupakan topik yang sangat menarik dalam ilmu komputer dimana kita temukan aplikasi susunan struktur data. dan topik kita kali ini adalah evaluasi dari operasi aritmatika dan ekspresi logic.

bagaimana cara kita menuliskan sebuah ekspresi?
contohnya:
A+B*C
2 + 5 * 3
Keterangan: A ,B ,C ,2 ,3 ,5 adalah Operand.
+,*  adalah Operator.


  Dalam struktur data yang kita pelajari secara umum ada 3 notasi operasi yang dilakukan untuk suatu operasi aritmatika,yaitu Prefix,Infix,dan postfix.Dan untuk mengetahui notasi-notasi yang diatas itu,sebelumnya kita harus mengenal dan mengetahui indikator yang ada di notasi itu tersebut.

Notasi ini terbentuk dari Operand dan Operator.
Operand adalah data atau nilai yang membantu dalam proses,sedangkan Operasi adalah fungsi yang digunakan dalam proses.

Notasi ada 3 jenis, yaitu Prefix,Infix dan Postfix yang seperti kita ketahui di atas:

1.Prefix adalah notasi yang terbentuk atas operator dengan operand, dimana oprator didepan operand.
 contoh: A + B * C (infix).
 maka notasi prefixnya adalah: +A*BC.

 Pemecahannya:

   A+B*C

  Diketahui ada 3 operand yaitu: A, B, C dan 2 operand yaitu: +, *.proses dimulai dengan melihat dari hirarkhi oprator.Contoh diatas operator yang tertinggi adalah * kemudian +. Tanda * diapit oleh 2 operand yaitu B*C, prefixnya dengan menggabungkan operand dan memindahkan operator ke depan dari operand,sehingga fungsi B*C, notasi prefixnya menjadi *BC.

Sehingga hasil sementara dari notasi prefix adalah:
   A+*BC

  Selanjutnya mencari prefix untuk operator yang berikutnya yaitu  +, cara yang dilakukan sama seperti diatas, operator + diapit oleh operand, yaitu A dan *BC, gabungkan operand,sehingga menjadi A*BC,lalu pindahkan operator kedepan operand,sehingga hasil akhir menjadi :
  +A*BC.

jika digambarkan :


2.Infix adalah notasi yang membentuk atas operator dengan operand,dimana operator berada diantara operand.
 Contoh :
      - A + B * C
      - (A + B) * C
      - A - (B + C) * D


3.Postfix adalah notasi yang membentuk atas operator dengan operand, dimana operator berada dibelakang operand.
 Contoh : A + B * C ( infix).
maka notasi postfix adalah ABC*+.

Pemecahannya:

      A + B * C

   Diketahui ada 3 operand yaitu : A,B,C dan 2 operator yaitu : +, *. proses dimulai dengan melihat dari hirarkhi operator.Contoh diatas operator yang tertinggi adalah * kemudian +.

Tanda * diapit oleh kedua operand yaitu B dan C yaitu B*C, postfix dengan menggabungkan operand B dan C menjadi BC,lalu memindahkan operator ke belakang operand C, sehingga fungsi B*C, notasi postfixnya menjadi BC*.Sehingga hasil sementara dari notasi postfix adalah A + BC*

  Selanjutnya mencari postfix untuk operator yang berikutnya, yaitu +, dengan cara yang dilakukan sama seperti di atas, operator + diapit oleh 2 operand, yaitu : A dan BC* gabungkan operand tersebut,sehingga menjadi ABC*,lalu pindahkan operator + kebelakang operand ABC*.
Sehingga hasil akhir  menjadi :   ABC*+.

Contoh Notasi Huruf :

Contoh Notasi Angka:

Read More

Struktur Data - Python : Graph

Salam semangat sobat kodingers 😁 semoga selalu dalam keadaan semangat yang menggebu  - gebu untuk ngoding yaa 😂. Yup kami kembali lagi dengan materi baru tentunya tak kalah menarik dari postingan - postingan sebelumnya 😁.  Kali ini kami akan membahas tentang graph. Kira - kira seperti apa ya graph itu? 😁. Langsung saja yuk kita simak 😄.

Graph

Sebelum kita bahas lebih lanjut, perhatikan gambar huruf a - e yang saling berhubungan di atas. Bagaimana setelah kalian melihat gambar di atas? Terbesitkah di benak kalian bagaimana ya caranya untuk menuliskan algoritma pemrogramannya ke dalam ex. Pyhon? Bagaimana juga ya cara mengetahui ada berapa jalur alternatif yang lebih singkat untuk di lewati? 

Sebelum kita melihat algoritmanya, perlu diperhatikan definisi graph secara singkat ialah metode pemetaan data dengan memberikan informasi pada kumpulan titik (node) yang dihubungkan dengan segmen garis. Titik atau node disebut verteks, sedangkan segmen garis disebut dengan ruas (edge). 

Algoritma pemrograman yang diimplementasikan ke dalam bahasa Pyhton beserta penjelasannya (disetiap baris code) bisa di perhatikan gambar di bawah ini : 

Algoritma all_path (seluruh jalur keseluruhan)

Algoritma shortest_path (jalur alternatif)

Algoritma menampilkan semua jalur

Pembentukan graph dan pemanggilan

Output dari graph di atas

Sekian materi graph yang bisa kami sampaikan, mohon maaf apabila terdapat kekeliruan dalam pengetikan algoritmanya, kami menerima saran dari kalian langsung saja komentar di kolom komentar di bagian bawah postingan ini 😁. Sampai jumpa di lain kesempatan ya sob. See youuu 😍.

Read More

Struktur Data - Python : Tree

Assalamu'alaikum sobat kodingers 😁, gimana nih kabar kalian? semoga dalam keadaan sehat dan selalu kuat ngoding yah 😂. Setelah lumayan lama tidak posting, kali ini kami kembali dengan postingan baru yang akkan membahas tentang "Tree" dalam struktur data. Kira-kira tree itu apa ya kok seperti pohon? 😂. Untuk lebih jelasnya yuk langsung saja kita simak 👂.

Tree

Pada postingan-postingan sebelumnya kita telah belajar mengenai menyimpanan data secara linear, seperti hasing, stack, queue dan linked list. Pada postingan kali ini kita akan mempelajari Tree yang memiliki cara penyimpanan data non-linear melainkan secara hierarki. Bagaimana maksudnya? Untuk mempermudahnya kita bayangkan saja susunan keluarga yang kita miliki. Jika diperhatikan dalam susunan tersebut kita akan menemukan siapa kakek kita, orang tua kita, saudara orang tua atau paman kita, sepepupu kita, saudara kita, atau bahkan cucu kita bukan? Begitulah kira - kira penggambarannya dari pengertian Tree penyimpanan data secara hierarki yang tersusun secara urut dari kakek hingga cucu. Berikut atribut - atribut yang terdapat dalam Tree :

1. Node: Serupa dengan simpul, node merupakan kerangka dasar dari sebuah tree (pohon), kadang disebut sebagai "key". Sebuah node dapat mengandung informasi tambahan (atau payload), meskipun informasi dalam node ini tidak wajib tetapi sangat penting dalam implementasi struktur data tree.
2. Edge: Garis penghubung antara dua buah node yang menunjukkan adanya relasi (hubungan) diantara kedua node. Setiap node (kecuali node root) terhubung dengan satu penguhubung yang menuju ke dalam node dan beberapa penghubung yang mengarah keluar dari node.
3. Root: Satu-datunya node dalam tree yang tidak memiliki garis penghubung (edge) yang mengarah ke dalam root, edge yang menghubungkan root semua mengarah ke luar dari node. (cikal-bakal)
4. Path: Jalur yang menghubungkan antara satu node dengan node yang lain, dapat dterdiri dari beberapa node dan edge yang berkesinambungan.
5. Children: Node yang terhubung dengan edge yang mengarah ke dalam node disebut children (selalu memiliki parent)
6. Parent: Node yang terhubung dengan edge yang mengarah keluar (memiliki anak).
7. Sibling: Node-node yang memiliki parent yang sama.
8. Subtree: Sekelompok node beserta turunnanya (anak-anaknya).
9. Sebuah node yang tidak memiliki children (anak)

Berikut implementasinya dalam bahasa pemrograman Python beserta penjelasannya pada beberapa baris : 

Output :

Dari output di atas dapat diartikan bahwa "a" bertindak sebagai parent/root, "b" merupakan anak kiri dan "c" merupakan anak kanan. Sebagai tambahan referensi, ada 3 metode penelurusan Tree yang dikenal dengan Tree Traversal yang akan kita bahas secara singkat saja. Yuk langsung saja ek tkp 😁.

Tree Traversal

Ada tiga pola umum yang digunkaan untuk mengunjungi semua node dalam tree. Perbedaan antara 3 pola ini adalah urutan kunjungan terhadap node. Kunjungan   ini dinamakan “traversal.”, yaitu preorder, inorder dan postorder. Berikut ini adalah definisinya :

• Preorder: Penelusuran node berawal dari ROOT, kemudian berlanjut ke turunan dari sebelah kiri, jika sedah jalur kiri sudah tidak ada anak lagi, diteruskan ke jalur turunan sebelah kanan, terus berlanjut sampai akhir node. Atau pertama menujuke node ROOT kemudian secara recursive mealkukan preorder pada subtree sebelah kiri, diikuti dengan traversal preorder secara recursive ke subtree sebelah kanan.
• Inorder: Melakukan traversal inorder secara recursive pada subtree sebelah kiri, menuju ke node ROOT, dan terakhir melakukan traversal inorder secara recursive pada subtree sebelah kanan.
• Postorder: Melakukan traversal postorder secara recursive pada subtree bagian kiri dan kanan diikuti dengan berkunjung ke node ROOT.

Implementasi algoritma ketiganya dalam Python seperti berikut :

Kira - kira seperti itulah materi yang bisa kami sampaikan hari ini 😁 mengenai Tree. Stay tuned pada postingan - postingan selanjutnya karena masih ada materi yang akan kami bagikan. Semoga bermanfaat, sampai jumpaaaa gaes 😁. Wassalamu'alaikum Wr. Wb.

Read More

Struktur Data : Linked list in python

Dalam struktur “Struktur data dalam Python” ini, saya akan membahas struktur data utama sering muncul dalam segala jenis pekerjaan insinyur / wawancara magang yaitu linked list

Apa itu linked list?

ini adalah gambaran dari linked list. ada 2 hal penting yang harus di perhatikan:
1. Sebuah linked list berisikan node.

2. Setiap node berisikan value (nilai) dan penunjuk (panah) ke node lain.

value

penunjuk

node di paling awal dalam linked list biasa disebut dengan header.

pada dasarnya linked list adalah rangkaian nilai yang terhubung dengan penghubung (pointer).

Mengapa harus menggunakan Linked List?

Linked list sering dibandingkan dengan array (list). Sedangkan array adalah ukuran tetap dari rangkaian, daftar yang ditautkan dapat memiliki elemen untuk dialokasikan secara dinamis. Apa pro dan kontra dari karakteristik ini? Berikut beberapa hal yang utama:

Keuntungan

Linked list dapat menghemat memori. Dia hanya mengalokasikan memori yang diperlukan untuk nilai yang akan disimpan. Dalam array, Anda harus mengatur ukuran array sebelum mengisinya dengan nilai, yang berpotensi membuang memori.

Node linked list dapat tinggal di mana saja dalam memori. Sedangkan array membutuhkan urutan memori yang akan dimulai, selama referensi diperbarui, setiap node dalam linked list dapat dipindahkan secara fleksibel ke alamat yang berbeda.

Kerugian

Ketika mencari nilai dalam linked list, Anda harus mulai dari awal rantai, dan periksa satu elemen pada suatu waktu untuk nilai yang Anda cari. Jika linked list n memiliki elemen panjang, ini bisa memakan waktu hingga n time. Sebaliknya banyak bahasa memungkinkan pencarian konstan dalam array.

penerapan linked list:
untuk kelas node

class Node:
    def __init__(self,val):
        self.val = val
        self.next = None # the pointer initially points to nothing

setelah memiliki kelas node kita bisa mengimplementasikan linked list berikut:

node1 = Node(12) 
node2 = Node(99) 
node3 = Node(37) 

node1.next = node2 # 12->99
node2.next = node3 # 99->37

# the entire linked list now looks like: 12->99->37

Anda mungkin bertanya-tanya mengapa saya tidak menerapkan kelas LinkedList. sebenarnya, linked list hanyalah sekelompok node yang terhubung bersama. Kami dapat merujuk ke header node sebagai linked list awal. Dalam contoh di atas, node1 adalah header node, dan itu juga dapat mewakili posisi dimulainya linked list.

Read More

Struktur Data - Python : Stack, Queue & DeQueue

Hai hai hai pencinta kodingan maupun yang masih ingin belajar 😆. Jumpa lagi pada postingan kali ini yang akan membahas tentang antrian dalam memasukan ataupun mengeluarkan data. Ada 3 metode yang akan kita bahas pada postingan kali ini, yang pertama Stack, yang kedua Queue dan yang terakhir DeQueue. Langsung saja yuk simak baik - baik 😄.

Stack

Tumpukan (stack) merupakan struktur data yang menerapkan konsep LIFO (Last In First Out) Artinya, data yang terakhir ditambahkan ke dalam stack akan berada di posisi terkahir (atau paling atas jika kita membayangkan elemen - elemen stack tersusun secara vertikal) dan ketika proses pengambilan, data terakhir tersebut akan diambil pertama kali.

Pada kelas di atas, kita mengimplementasikan metode-metode berikut :

1. isempty(), digunakan untuk memeriksa apakah stack kosong atau tidak.
2. __len__(), metode ini perlu diimplementasikan agar objek dari kelas stack dapat dihitung
    jumlah elemennya menggunakan metode len().
3. push(), digunakan untuk menambah elemen baru ke dalam stack pada posisi terakhir.
4. peek(), digunakan untuk mendapatkan elemen yang terdapat pada posisi terkahir tanpa
    menghapus elemen tersebut.
5. pop(), digunakan untuk mengambil elemen terakhir dan menghapusnya dari dalam stack.
6. size(), mengembalikan jumlah item di dalam list. Tidak memerlukan parameter dan
    mengembalikan suatu integer.

Setelah kalian sudah paham, kalian dapat mengembangkan kelas stack di atas untuk menambah kemampuan - kemampuan lain yang diperlukan, seperti penambahan kapasitas elemen di dalam list, pencarian elemen list di dalam list, dan sebagainya. Jika sudah kalian mencobam jangan lupa sharekan link mu di kotak komentar di bawah ya 😁. Sekarang  langsung saja implementasinya ke dalam Phyton :

Outputnya 

Seperti kira - kira untuk materi stack, selanjutnya kita akan membahas Queue, yuk langsung saja ke tkp 😁.

Queue

Antrian (queue) merupakan struktur data yang menerapkan konsep FIFO (First In First Out), berbanding terbalik dengan (stack) yang memiliki konsep data yang masuk paling belakang akan keluar terlebih dahulu. Data atau elemen yang pertama ditambahkan ke dalam queue akan diambil pertama kali juga seperti pada ilusrasi di atas.

Pada kelas queue di atas, kita mengimplentasikan metode - metode berikut :

1. isempty(), digunakan untuk memeriksa apakah queue kosong atau tidak.
2. enqueue(), digunakan untuk menambah elemen baru ke dalam queue pada posisi terakhir.
3. peek(), digunakan untuk mendapatkan elemen yang terdapat pada posisi terkahir tanpa
  menghapus elemen tersebut.
4. dequeue(), digunakan untuk mengambil elemen terakhir dan menghapusnya dari dalam
  queue.
5. size(), mengembalikan jumlah item di dalam list. Tidak memerlukan parameter dan
   mengembalikan suatu integer.
6. semua(), mengecek isi list Queue.

Berikut implementasinya ke dalam bahasa pemrograman Python :

Output :

Seperti itulah kira - kira materi Queue yang bisa kami sampaikan 😁, nanti pada akhir materi setelah kita membahas DeQueue, akan kami beri contoh penerapan Stack dan Queue dalam game atau pun dalam bentuk lainnya. Jadi simak terus yah 😁.

DeQueue

DeQueue, dikenal juga sebagai antrian berujung dua (double-ended), adalah suatu koleksi item terurut serupa dengan queue. Perbedaannya? Sifat tidak terikat untuk penambahan dan penghapusan item-item dari antrian. Item baru dapat ditambahkan ke depan atau belakang. Karena itu, item yang ada dapat dihapuskan dari salah satu ujung. Struktur linier hibrida ini menyediakan semua kapabilutas stack dan antrian dalam satu struktur data.

Berikut ini adalah beberapa operasi yang dapat diberlakukan terhadap Deque :

1. deque(), membuat suatu deque baru yang kosong. Tidak perlu parameter dan
    mengembalikan suatu deque kosong.
2. addFront(item), menambahkan suatu item baru ke depan dari deque. Perlu item dan tidak 
    mengembalikan apapun.
3. addRear(item), menambahkan suatu item baru ke ekor dari deque. Perlu item dan tidak
    mengembalikan sesuatu.
4. removeFront(), menghapus item depan dari deque. Tidak perlu parameter dan 
    mengembalikan item. Deque termodifikasi.
5. removeRear(), menghapus item ujung (ekor) dari deque. Tidak perlu parameter dan
    mengembalikan item. Deque berubah.
6. isEmpty(), menguji apakah deque dalam kondisi kosong. Tidak perlu parameter dan 
    mengembalikan suatu nilai boolean.
7. size(), mengembalikan jumlah item dalam deque. Tidak perlu parameter dan 
    mengembalikan suatu integer.

Untuk lebih jelasnya, langsung saja kita implementasikan ke dalam bahasa pemrograman Python seperti berikut :

 Output :

Itulah sekilas materi tentang DeQueue, semoga teman - teman bisa memahaminya yaa 😁, jangan lupa langsung saja di praktekan agar tambah mengerti. Oh iya hampir lupa 😂 nih, sesuai janji saya tentang contoh penerapan Stack dan Queue dalam permainan seperti apa, langsung saja perhatikan algoritma di bawah ini.

Permainan Simulasi Tangkap Nama :

Output :

Palindrome dalam kata :

Output :

Semoga bermanfaat, sampai jumpa pada postingan selanjutnya yaa 😁, byeeeee.

Read More

Struktur Data : Hashing Python

Haloo sobat kodingers, kembali lagi bersama saya 😅. pada postingan sebelumnya kita telah membahas tentang searching dan sorting. kali ini kita akan melangkah lebih maju dengan membentuk struktur data yang disebut "hashing".

Untuk melakukan ini, kita perlu tahu lebih banyak tentang di mana barang-barang yang memungkinkan untuk kita cari dalam koleksi. Jika setiap item berada di tempat yang seharusnya, maka pencarian dapat menggunakan perbandingan tunggal untuk menemukan keberadaan suatu item. Akan tetapi, ini bukan kasusnya.

Tabel hash adalah kumpulan item yang disimpan sedemikian rupa untuk memudahkan menemukannya nanti. Setiap posisi tabel hash, sering disebut slot, dapat menyimpan item dan diberi nama oleh nilai integer mulai dari 0. Sebagai contoh, kita akan memiliki slot bernama 0, slot bernama 1, slot bernama 2, dan seterusnya di. Awalnya, tabel hash tidak berisi item sehingga setiap slot kosong. Kita dapat mengimplementasikan tabel hash dengan menggunakan daftar dengan setiap elemen diinisialisasi dengan nilai None. Gambar di bawah ini akan menunjukkan tabel hash berukuran m = 11. Dengan kata lain, ada slot m di dalam tabel, berindex 0 hingga 10.

index	0	1	2	3	4	5	6	7	8	9	10
value	77	None	None	None	26	93	17	None	None	31	54

Pemetaan antara item dan slot tempat item yang termasuk dalam tabel hash disebut fungsi hash. Fungsi hash akan mengambil item apa pun dalam koleksi dan mengembalikan integer dalam kisaran nama slot, antara 0 dan m-1. Asumsikan bahwa kita memiliki set item integer 54, 26, 93, 17, 77, dan 31. Fungsi hash pertama kami, kadang-kadang disebut sebagai "metode sisa," hanya mengambil item dan membaginya dengan ukuran tabel, mengembalikan sisanya sebagai nilai hashnya (h (item) = item% 11). Tabel 4 memberikan semua nilai hash untuk contoh item kami. Perhatikan bahwa metode sisa ini (aritmatika modulo) biasanya akan hadir dalam beberapa bentuk di semua fungsi hash, karena hasilnya harus dalam kisaran nama slot.

item%11 (11 adalah banyaknya slot yang kita buat sisa dari mod tersebut akan dijadikan index untuk menempatkan item yang kita buat)

item	index
54	10
26	4
93	5
17	6
77	0
31	9

Sekarang ketika kita ingin mencari item, kita cukup menggunakan fungsi hash untuk menghitung nama slot untuk item dan kemudian periksa tabel hash untuk melihat kosong tidaknya tabel tersebut. ketika dalam tabel berisikan None. maka, akan dimasukkan angka yang telah ditentukan indexnya.

mungkin kalian akan bertanya bagaimana jika ada index yang bertabrakan kan?. take it easy 😅
hal tersebut biasa dinamakan collision (tabrakan) ketika item bertabrakan ada beberapa metode yang dapat kita gunakan antara lain ada open addressing dan close addressing. open addressing terdiri dari linier hashing dan kuadratic hashing. sedangkan close addressing berdiri sendiri.

sekarang kita bisa membuat permisalan atau list baru

item	index
54	10
44	4
93	5
17	6
77	0
55	0

dalam list tersebut terdapat 2 value dengan posisi index yang sama (77 dan 44 pada index 0) dalam kondisi ini terjadi tabrakan atau collision. bagaimana penyelesaiannya? pertama kita akan selesaikan menggunakan linier hashing kemudian akan dilanjut dengan binary hashing dan close address.

Linier Hashing

linier hashing adalah cara penyelesaian collision pada hashing dengan memindahkan angka yang collision dengan index_collision=index_collision+1%panjang_index sehingga ketika ada collision pada index 0(seperti contoh) maka akan di tempatkan pada 0+1%panjang_index maka, akan ditempatkan pada index 1. namun saat pada index 1 terdapat item didalamnya maka akan bergeser lagi pada index 1+1%panjang_index (index menjadi 2) begitu seterusnya.

index	0	1	2	3	4	5	6	7	8	9	10
value	44	77	55	None	None	93	17	None	None	None	54

Binary Hashing

binary hashing adalah cara penyelesaian collision pada hashing dengan memindahkan angka yang collision dengan index_collision=index_collision+(i**2)%panjang_index (i bermula dari angka 1 dengan increment +1) sehingga kita akan tempatkan item yang bertabrakan pada index +(1**2,2**2,dst) hingga menemukan posisi yang kosong.

index	0	1	2	3	4	5	6	7	8	9	10
value	44	77	None	None	55	93	17	None	None	None	54

dapat kita lihat perbedaan pada penempatan index dengan value 55 pada list tersebut. pada Linier hashing value 55 terletak pada index 2. sedangkan pada binary hashing value 55 terletak pada index ke 4.

Close Address
close address adalah cara penyelesaian collision pada hashing dengan menyatukan item-item collision dalam list baru sehingga tidak perlu bergeser-geser lagi. pada data di atas akan didapat 3 item yang collision pada index 0. dengan menggunakan metode close address akan didapati pada index ke 0 berisi [44,77,55]

index	0	1	2	3	4	5	6	7	8	9	10
value	[44,77,55]	None	None	None	None	93	17	None	None	None	54

Read More